Understand Recurrent Neural Network with Keras
Introduction
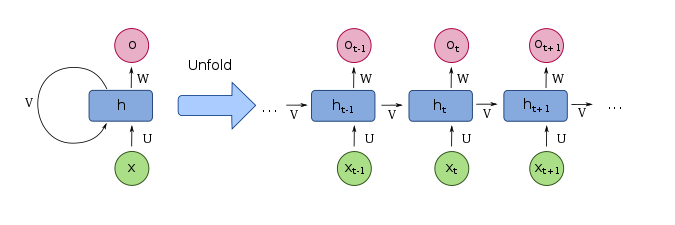
A recurrent neural network (RNN) is a neural network with a feedback loop. Contrary to a standard neural network, a sample got an extra dimension, a sequencing. In Keras, it is called timestep dimension.
This kind of network aims to keep in mind its states accross the timesteps.
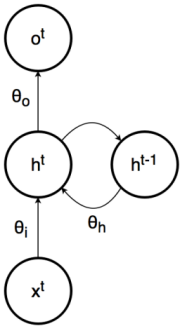
The fundamental equations of a simple RNN expressed at the current timestep \(t\) are:
Where \(o\) is the output, \(h\) the hidden state and $x$ the input. \(\theta\) are the weights to be adjusted of the RNN. \(f,g\) are activation functions, as sigmoid, Relu…
implementation
This post outlines Keras implementation of a very simple RNN is able to add octets (8 bits binary numbers). This example is perfect to understand what a recurrent networks are designed for; keep hidden state in memory. Here, we want the RNN to be able to add the carry bit.
I have been inspired by the great explanation found here This page gives RNN code step by step, giving good insight of how the back-propagation works for this kind of network.
A sample \(x\) is made of two octets and the output \(o\) is the addition result one. For instance; \(x = [[00110010], [00010010]]\) and \(o=[01000100]\)
from keras.models import Sequential
from keras.layers.core import Dense
from keras.layers.wrappers import TimeDistributed
from keras.layers.recurrent import SimpleRNN
from keras.utils import np_utils
from keras.optimizers import SGD
import keras.backend as K
First, let us generate a binary mapper and a integer mapper
seed = np.random.seed(0)
# int2binary
int2binary = {}
binary_dim = 8
largest_number = pow(2,binary_dim)
binary = np.unpackbits(
np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
for i in range(largest_number):
int2binary[i] = binary[i]
# binary2int
def binary2int(b):
out = 0
for index,x in enumerate(b):
out += x*pow(2,index)
# print(out)
return out
We can now convert easily any integer smaller than 256 to binary representation. For our addition problem, we limit the inputs number to being smaller than 128 in order to keep the output smaller than 256.
# example of binary mapper
a_int,b_int = np.random.randint(largest_number/2,size = 2)
c_int = a_int + b_int
x = np.stack([int2binary[a_int],int2binary[b_int]])
o = int2binary[c_int]
print('inputs %s \n output %s'%(x,o))
inputs [[0 0 1 0 1 1 0 0]
[0 0 1 0 1 1 1 1]]
output [0 1 0 1 1 0 1 1]
We have to keep in mind to reverse the inputs so as to feed the RNN with first small bit coding \(2^0\)
# input variables
alpha = 0.1
input_dim = 2
hidden_dim = 16
output_dim = 1
nb_ex = 10**5
model = Sequential()
model.add(SimpleRNN(hidden_dim, name='rnn',
input_shape=(binary_dim,2),
stateful=False,
activation='sigmoid',
return_sequences=True,
use_bias =False))
model.add(TimeDistributed(Dense(units = 1,name='output',
activation ="sigmoid",
use_bias=False)))
model.summary()
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
rnn (SimpleRNN) (None, 8, 16) 288
_________________________________________________________________
time_distributed_10 (TimeDis (None, 8, 1) 16
=================================================================
Total params: 304.0
Trainable params: 304
Non-trainable params: 0.0
_________________________________________________________________
How wen can see, we have 304 parameters to train. In fact, there is:
\(\theta_i\) has 2x16 weights
\(\theta_h\) has 16x16 weights
\(\theta_o\) has 16x1 weights
To keep close to this implementation again, we look at the sum of the absolute error of the output neuron over the 8 timestamps.
Insteed of using the mean square error loss: \(C = \frac{(y-a)^2}{2}\)
we can use the binary cross entropy of Keras. \(C = - y \ln a + (1-y ) \ln (1-a)\)
The cost function computed at each timestamp is now:
# custom metrics to show
def overall_error(y_true,y_pred):
return K.sum(K.abs(y_true-y_pred))
# stochastic gradient descent strategy
sgd = SGD(lr=alpha, momentum=0.0, decay=0.0, nesterov=False)
# loss: binar
model.compile(loss='binary_crossentropy', optimizer=sgd,
metrics=[overall_error])
for ex in range(nb_ex):
# data shape = (steps, inputs/outputs)
a_int,b_int = np.random.randint(largest_number/2,size = 2)
c_int = a_int + b_int
X_ex = np.stack([int2binary[a_int],int2binary[b_int]]).T
# reverse the inputs; to feed the RNN with first bits
X_ex = np.reshape(X_ex[::-1],(1,binary_dim,2))
Y_ex = int2binary[c_int]
Y_ex = np.reshape(Y_ex[::-1],(1,binary_dim,1))
#a gradient descent at each example
loss,metrics = model.train_on_batch(X_ex, Y_ex)
ex += 1
if ex % 10**4 == 0:
pred = model.predict_on_batch(X_ex).round()
pred_int = binary2int(np.reshape(pred,binary_dim))
print('%s+%s?=%s'%(a_int,b_int,pred_int))
print(loss)
34+54?=4.0
0.641955435276
78+109?=187.0
0.0652224719524
51+94?=145.0
0.020537737757
47+48?=95.0
0.00928809680045
35+27?=62.0
0.00299859023653
101+100?=201.0
0.0025868860539
99+37?=136.0
0.0027393035125
65+106?=171.0
0.00234018452466
73+108?=181.0
0.0016108098207
114+71?=185.0
0.00154325680342
After 200 000 examples, the RNN knows how to add the carry bit. To be convinced of this, let’s try with “the most” difficult example, where the carry bit crosses the whole octet:
a_int = largest_number-2
b_int=1
X_ex = np.stack([int2binary[a_int],int2binary[b_int]]).T
print("input: \n %s"%X_ex.T)
X_ex = np.reshape(X_ex[::-1],(1,binary_dim,2))
pred = model.predict_on_batch(X_ex).round()
print("output: \n %s"%pred[0].T[::-1])
input:
[[1 1 1 1 1 1 1 0]
[0 0 0 0 0 0 0 1]]
output:
[[ 1. 1. 1. 1. 1. 1. 1. 1.]]
