Les réseaux de neurones pour l’image expliqués simplement

Cet article s’inspire d’une présentation que j’ai donnée à une classe de 3ème, dans l’objectif de leur faire comprendre comment l’étude du cerveau et des neurones permet de résoudre des problèmes en analyse d’image d’apparence complexes. Nous verrons que le seul prérequis est la maîtrise de l’addition et la multiplication. Les réseaux de neurones informatiques ne font rien de plus!

Introduction

On modélise la réalité en vu de simuler un phénomène physique réel et souvent complexe. On utilise des modèles pour leur pouvoir prédictif, pour répondre à des questions. Va t-il pleuvoir dans l’heure? La route pour rentrer chez moi sera dégagée? Le pont va t-il s’écrouler? La courbe du chômage va t-elle descendre?

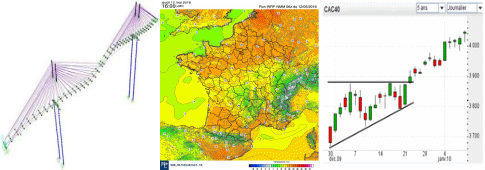
Ces modèles résolvent des équations qui décrivent le système à modéliser. Quand la solution des ces équations est inconnues, les ingénieurs font des approximations, ou bien découpent le système en petit bouts (spatial, temporel…) sur lesquels un calcul est possible.

Pour la classe de problème qui va faire l’objet de cet article, c’est à dire l’analyse d’image; comment les résoudre?

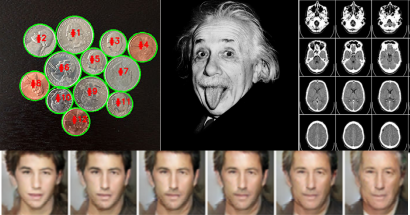
Par exemple; dans les images ci dessous, comment trouver des équations, des modèles qui répondent à ces questions? Combien de pièces de monnaies? A qui est cette langue? Ce cerveau est-il atteint d’une tumeur? Comment le visage de cet enfant va évoluer?

Ces questions se sont posées depuis l’apparition des premiers ordinateurs dans les années 1980, capables de stocker des images . Les scientifiques à cette époque, ont imaginés toute sorte de modélisation, avec beaucoup de traitement d’image afin de construire des règles simples. Par exemple, dans le domaine de reconnaissance faciale, des dizaines d’équipes de recherche, se sont employées à trouver les yeux, le nez, les oreilles, puis à comparer des distances entre eux pour identifier l’individu.

Vous l’avez compris, l’analyse d’image n’est pas régit par des équations physiques; les solutions basées sur des règles arbitraires marchent mal.

Pourtant, une abeille sait reconnaître sa ruche , un aigle repère sa proie à un kilomètre de distance. Comment font-ils et surtout, comment pouvons nous les imiter pour nos problèmes de vision assistée par ordinateur?

C’est là que les réseaux de neurones entrent en scène !

Avant de rentrer dans notre cerveau, une petite perspective historique est bienvenue:

• 300 av. JC : Le siège de la pensée était le cœur (Platon)
• 13ème : La dissection de nouveau autorisée
• 18ème : Invention du microscope (zoom optique x300)
• 1839: invention de la photographie
• 1900 : Introduction du neurone, messages nerveux ¹
• 1950 : Découverte des champs récepteurs dans l’œil de la grenouille
• 1970 : Premiers réseaux de neurones informatique
• 2000 : Réseaux profonds grâce à l’augmentation des performances des ordinateurs
• 2015 : C’est la mode !

Le neurone simple

Bien que le cerveau présente encore des mystères, on sait qu’il est le centre de calcul du corps; c’est la que les décisions sont prises, comme de lever un bras. Le cerveau est relié au reste du système nerveux par la moelle épinière, qui collecte et transmet les informations venant des membres et les ordres venant du cerveau.

Formant des systèmes spécialisés dans des endroits précis du crâne, ils sont dédiés à l’image (lobe occipital), l’autre au texte…

Chacune de ces zones est composée de neurones et agissent comme des petits ordinateurs.

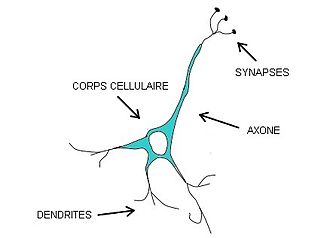
Leur jeu préféré est de se transmettre de l’information via des signaux électriques, puis de l’amplifier ou de l’atténuer. ils possèdent deux types de prolongements bien particuliers qui les distinguent des autres cellules.

1. Les dendrites, qui se divisent comme les branches d’un arbre, recueillent l’information et l’acheminent vers le corps de la cellule.

2. L’axone, généralement très long et unique. Cet axone conduit l’information du corps cellulaire vers d’autres neurones avec qui il fait des connexions appelées synapses. Les axones peuvent aussi stimuler directement d’autres types de cellules, comme celles des muscles ou des glandes.

Le neurone de base peut donc être modélisé de cette manière. Soit x1, x2 et x3. l’intensité du signal électrique des dendrites et y celui à sortie du synapse. Notre neurone possède des poids w1, w2 et w3 qui augment ou diminuent les intensités x. Enfin le signal résultant z est filtré s’il n’est pas assez grand. Dans le cas contraire, le neurone est dans un état excité et sa sortie Y est non nulle.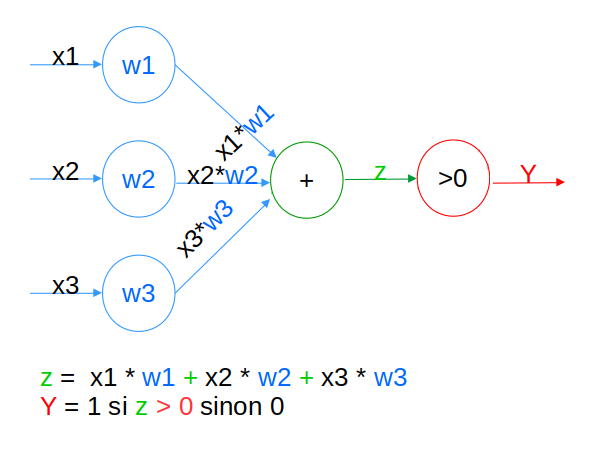

Ces neurones, proposés dès 1958 sont les plus simples à comprendre et à modéliser. En informatique, lorsqu’ils sont disposés côte à côte, il forme ce qu’on appelle une couche dense. Voyons à présent comment fonctionnent les neurones chargé de la vision.

Les neurones à champ récepteur

Pour voir, il faut d’abord que l’œil forme une image précise de la réalité sur la rétine. Il faut ensuite que l’intensité lumineuse soit transformée en influx nerveux par les cellules photoréceptrices de la rétine.

Ces cellules sensibles à la lumière qui tapissent la rétine, agissent comme des capteurs de couleur. Nous en avons de 4 sortes. 3 cônes pour le rouge, le vert et le bleu et des bâtonnets sensibles aux faibles contrastes de luminosité. Nous voyons le monde à travers ces filtres et le cerveau en fabrique une représentation coloré. Il crée même des couleurs qui n’ont aucune existence physique, comme le rose!

Le traitement de l’image par le système nerveux devient alors possible et il commence non pas dans le cerveau mais immédiatement dans la rétine elle-même. D’ailleurs, les anatomistes considèrent la rétine comme une partie du cerveau située à l’extérieur de celui-ci, un peu comme l’antenne de votre téléviseur située sur le toit fait partie intégrante de votre poste de télévision.

Dans la rétine se situe des neurones spécialisés dans des tâches simples et localisés. Ils sont excités quand leurs champs récepteurs, c’est à dire des cellules photoréceptrices proches, sont elles même stimulée par la portion d’image projetée à travers le cristallin (sorte de lentille).

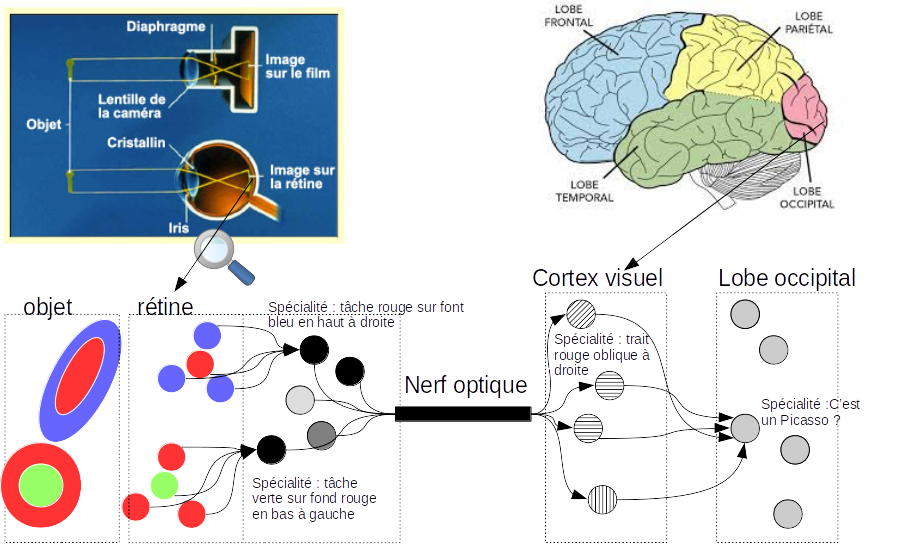
Admettons que vous soyez au musée devant un tableau composé d’un ovale rouge sur fond bleu en haut à droite, et d’un disque vert sur fond rouge en bas à gauche. Sur votre rétine des points rouge sur fond bleu apparaissent, ce qui excite des neurones spécialisés à reconnaître ce motif à cet endroit. Les stimulis résultants de ces neurones composent à leur tour le champ récepteur des neurones de la couche suivante dans le cortex visuel.

Au fur et à mesure, l’image formée sur la rétine se propage dans des couches empilés de neurones; l’image est compressée en quelque sorte et cette représentation peut servir pour des tâches spécialisés comme reconnaître un objet, une personne ou un mouvement.

Voyons maintenant comment imiter ces neurones avec du traitement par ordinateur. Devant des phénomènes si complexes, les chercheurs et bio-informaticiens ont simplifié; tant mieux!

Une image informatique

D’abord, il est primordial de bien comprendre ce qu’est une image en informatique. Contrairement aux premiers appareils photos, l’image prise d’une scène n’est pas continue, c’est à dire qu’elle est découpée en petits carrées. On les appelle les pixels.

Un pixel encode l’image en trois canaux (rouge, vert et bleu) avec un nombre généralement entre 0 (l’octet 0000 0000) et 255 (l’octet 1111 1111). Ainsi, une photo en couleur est la superposition de trois images en niveau de gris qui portent chacune une intensité de couleur primaire!

La photographie ci dessous est tirée d’un magasine PlayBoy de 1972. Elle a servie de test aux algorithmes de traitement d’image car elle possède des caractéristiques intéressantes, comme des régions uniformes et de textures variées.

Maintenant que l’on a compris ce que représente l’image (la donnée d’entrée du problème), nous allons s’inspirer du fonctionnent biologique de la rétine et du cortex visuel pour bâtir un modèle simple, qui extrait l’information. En fait, nous allons simplifier d’avantage en considérant une image en noir et blanc. La couleur n’est qu’une généralisation en plusieurs dimensions du problème.

D’ailleurs, dans la nature, les chiens voient en nuance de gris, alors que certaines espèces ont des cellules photoréceptrices d’un type particulier pour capter d’autres niveaux de couleur!

Modélisation du neurone à champs récepteur

Imaginons un petit modèle extracteur de texture à quatre type de neurones, représenté par des filtres de 2x2 pixels auxquels on associe un seuil de coupure s, un nombre entier.

Considérons un bout d’image de 8x8 pixels sur lequel un motif se dessine en noir, que l’on découpe en 4 groupes rouge, jaune bleu et vert de 4x4 pixels. Par analogie avec la section précédente, ces groupes forment les champ récepteur des 4 neurones.

La réponse d’un neurone est positive quand au moins s pixels coincident avec ce champ récepteur.

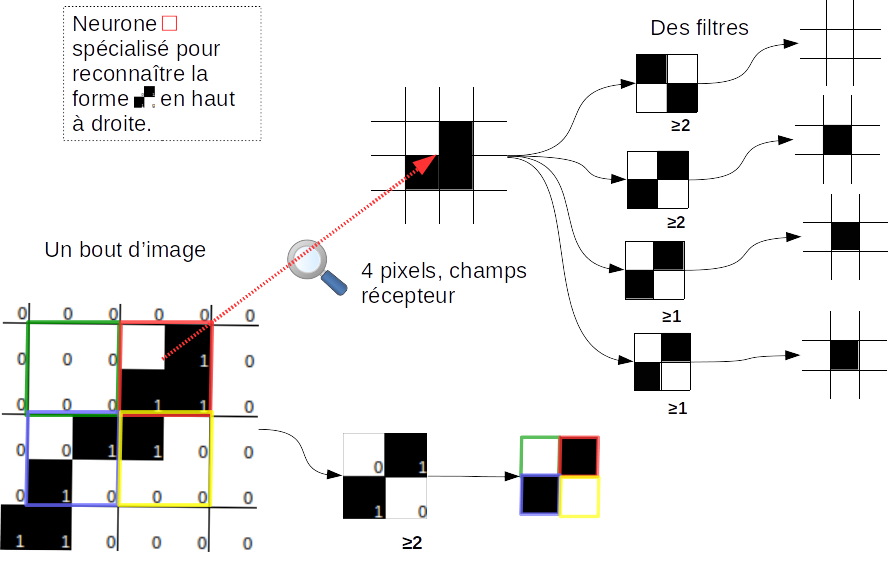
Sur l’illustration ci-dessous, on donne la réponse de l’image 8x8 à travers un des filtres diagonal avec un seuil de 2.

Comme par construction un neurone réduit la dimension spatiale de 2x2 pixels à 1x1 pixel, le bout d’image à travers les 4 neurones renvoie 4 cartes de réponse de taille 2x2.

On a crée ainsi une couche de neurones à champs récepteur, ou encore de convolution (C’est le terme technique employé) qui filtrent des motifs dans l’image.

Réduction de la dimension

Dans une image avec plus de pixels (en général plusieurs millions) et beaucoup de neurones de convolution, il peut être intéressant de compacter la réponse des couches successives. Cela permet d’avoir des modèles plus légers et plus même parfois plus performants!

L’idée ici est simple; on crée une couche tel que le neurone de sortie s’active seulement si au moins un neurone de son champ récepteur est excité.

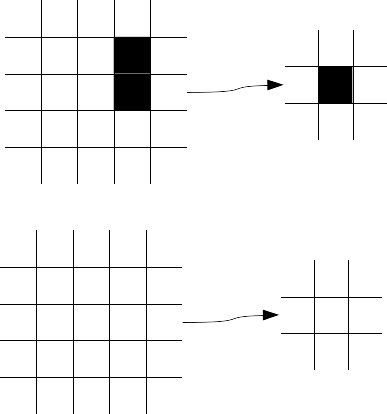
Modèle complet de réseau de neurone

Pour illustrer ce qui précède, prenons un exemple concret. Supposons une petite fonction d’un cerveau simple qui répond à la question :

Est-ce un carré ou un rond dans l’image?

Le modèle prend en entrée une image en noir et blanc de dimension 12x12 et retourne la sortie de son neurone final. Le modèle est construit de sorte que l’état de ce neurone dépende de l’entrée. Si la sortie est positive l’entrée est probablement une croix, sinon c’est un rond.

Ce modèle est une succession de 4 couches:

• Une couche de convolution avec 2 filtres de dimension 2x2.
• Une couche de réduction de dimension d’un facteur 2.
• Une couche de convolution avec 2 filtres de dimension 2x2.
• Une couche de réduction de dimension d’un facteur 2.
• Un neurone simple avec 4 dendrites et 2 synapses.

Voici le modèle avec une entrée (un rond ici) et la réponse de chaque couche. Les couches dans les boites rouges sont des convolutions et les couches dans des boites vertes sont des réductions de dimension.

On peut remarquer que les filtres de la première couche discriminent les motifs diagonaux dans les 8x8 champs récepteurs de l’image. Pour un rond, on s’attend donc à avoir des signaux positifs en haut droite et en bas à gauche de la carte de réponse du premier filtre. Pour une croix, cela serait l’inverse.

Ce réseau de neurone a besoin de garder en mémoire persistante les pixels des filtres (6 filtres de taille 2x2 +1 seuil) et 4 poids de dendrites et un seuil. C’est à dire un total de 35 éléments.

Pour fonctionner, il lui faut un espace de mémoire vive de la taille de l’image, plus la taille des des cartes de réponses des filtres de convolution ainsi que les réponses des couches de réduction et enfin de l’état du dernier neurone simple. Soit 229 éléments.

Notre modèle pourrait donc être implémenté sur un ordinateur léger et peu performant.

Un modèle vierge est disponible ici.

Conclusion

Nous avons vu avec un exemple très simple comment un réseau de neurone appliqué à l’image pouvait fonctionner informatiquement. Il faut maintenant imaginer un modèle similaire avec des centaines de couches successives, beaucoup plus de filtres par couche (au moins 30) et une meilleure résolution d’image en entrée, si possible en couleur!

Vous obtiendrez un réseau profond capable de classifier des visages ou des objets. D’autres réseaux sur le même principe, moyennant tout de même quelques modifications pourront détecter des objets en plus de les classifier.

Des architectures encore plus élaborées poussent encore plus loin les possibilités de traitement d’image; cependant elles sont bâties avec des couches similaires.

Une question cruciale nous vient à présent à L’esprit: si on comprend comment le réseau propage l’information à travers de nombreuses couches pour obtenir une réponse, comment fixer les poids des neurones qui les composent?

En fait, nous avons vu seulement la phase d’inférence du réseau où les paramètres sont déjà choisis.

Au préalable, une phase d’entraînement modifie ces paramètres petit à petit jusqu’à obtenir une convergence, en proposant des entrées pour lesquelles la réponse attendue est connue. Le réseau s’entraîne en valorisant les cas où sa réponse est correct et en punissant ses erreurs; mais cela fera l’objet d’un prochain article!

Reference